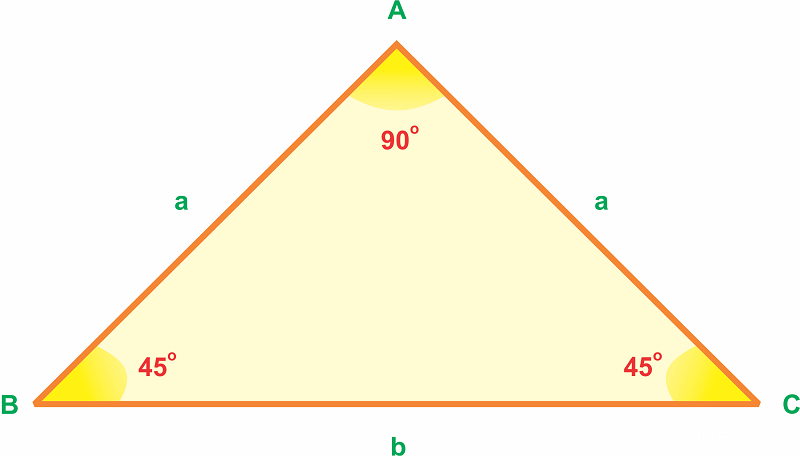
Diện tích tam giác vuông cân
Công thức
Chương trình hình học lớp 7 trong giáo dục phổ thông Việt Nam thường bao gồm các nội dung cơ bản sau đây:
Các khái niệm cơ bản về hình học:
Điểm, đường thẳng, đoạn thẳng.
Các loại góc (góc nhọn, góc vuông, góc tù, góc bẹt).
Đường trung trực của đoạn thẳng, phân giác của góc.
Tam giác:
Các loại tam giác (tam giác thường, tam giác cân, tam giác đều, tam giác vuông, tam giác vuông cân).
Tính chất các đường đặc biệt trong tam giác (đường trung tuyến, đường phân giác, đường cao, đường trung trực).
Các định lý về tam giác (định lý tổng ba góc trong tam giác, định lý Pythagore).
Các bài toán về tam giác:
Tính chu vi và diện tích tam giác.
Các bài toán về sự đồng dạng và bằng nhau của tam giác.
Ứng dụng của các định lý vào giải bài toán thực tế.
Tham khảo: Đề thi tiếng anh thpt quốc gia 2019 mã 401
Tứ giác:
Hình học thế giới
Các loại tứ giác (hình thang, hình thang cân, hình bình hành, hình chữ nhật, hình vuông, hình thoi).
Tính chất các loại tứ giác.
Tính chu vi và diện tích các loại tứ giác.
Đường tròn:
Khái niệm và các yếu tố liên quan đến đường tròn (bán kính, đường kính, cung, dây, cung lớn, cung nhỏ).
Tính chất của đường tròn và các định lý liên quan (đường kính vuông góc với dây, góc nội tiếp và góc ở tâm).
Tính chu vi và diện tích đường tròn.
Hình học không gian cơ bản (nếu có thời gian và chương trình mở rộng):
Khái niệm về hình hộp chữ nhật, hình lập phương.
Tính diện tích bề mặt và thể tích các khối đa diện cơ bản.
Một số điểm cần lưu ý:
Đảm bảo hiểu rõ và nắm vững các định lý và tính chất để áp dụng vào giải bài tập.
Thực hành vẽ hình chính xác và sử dụng các công cụ hình học như thước kẻ, compa.
Luyện tập giải các bài toán đa dạng để nắm chắc kiến thức.
Hy vọng thông tin trên sẽ giúp bạn nắm bắt được chương trình học hình học lớp 7
Diện tích của tam giác vuông cân là một kiến thức cơ bản trong hình học và có nhiều ứng dụng thực tế trong đời sống hàng ngày. Dưới đây là một số ví dụ về cách áp dụng diện tích tam giác vuông cân:
Thiết kế và xây dựng:
Lợp mái nhà: Mái nhà thường có dạng tam giác vuông cân để giúp thoát nước mưa tốt hơn. Tính diện tích mái nhà giúp xác định lượng vật liệu cần thiết như tấm lợp, gỗ, hoặc vật liệu cách nhiệt.
Bậc thang: Các bậc thang thường có dạng tam giác vuông cân. Tính diện tích giúp xác định lượng gỗ hoặc vật liệu cần thiết để làm các bậc thang.
Trang trí nội thất:
Trang trí tường: Khi trang trí tường với các mảng hình học, các miếng dán hoặc vải hình tam giác vuông cân có thể được sử dụng để tạo hiệu ứng thẩm mỹ.
Gạch lát sàn: Sử dụng các viên gạch hình tam giác vuông cân để lát sàn hoặc tường theo các mẫu thiết kế độc đáo.
Nông nghiệp và cảnh quan:
Vườn cây hoặc bãi cỏ: Khi thiết kế khu vườn hoặc bãi cỏ có các đường biên hình tam giác vuông cân, tính diện tích giúp xác định lượng hạt giống hoặc phân bón cần thiết.
Bồn hoa: Bố trí bồn hoa hình tam giác vuông cân trong các công viên hoặc khu vườn giúp tận dụng không gian và tạo điểm nhấn thẩm mỹ.
Nghệ thuật và thủ công:
Cắt giấy và vải: Trong các hoạt động thủ công như cắt giấy hoặc vải để làm thiệp, tranh hoặc đồ trang trí, tam giác vuông cân là một hình dạng cơ bản thường xuyên được sử dụng.
Gấp giấy nghệ thuật (origami): Nhiều mẫu gấp giấy nghệ thuật sử dụng tam giác vuông cân để tạo ra các hình dạng phức tạp hơn.
Toán học và giáo dục:
Bài tập và bài giảng: Giáo viên thường sử dụng các ví dụ về tam giác vuông cân để giải thích các khái niệm hình học, diện tích, và tỷ lệ trong các bài giảng.
Trò chơi và hoạt động học tập: Các trò chơi giáo dục và hoạt động học tập sử dụng các hình tam giác vuông cân để giúp học sinh hiểu và thực hành các khái niệm hình học.
Những ứng dụng này cho thấy tầm quan trọng và sự tiện dụng của việc hiểu và tính toán diện tích tam giác vuông cân trong nhiều lĩnh vực khác nhau của đời sống hàng ngày.
Ngành hình học đã có nhiều phát minh và đóng góp vĩ đại qua các thời kỳ, từ thời cổ đại đến hiện đại. Dưới đây là một số phát minh quan trọng và các nhà toán học nổi tiếng đã có những đóng góp vĩ đại trong ngành hình học:
Hình học Euclid:
Euclid: Euclid là một nhà toán học Hy Lạp cổ đại, được coi là "cha đẻ của hình học". Tác phẩm nổi tiếng nhất của ông, "Elements" (Các yếu tố), là một trong những công trình toán học có ảnh hưởng lớn nhất. "Elements" hệ thống hóa các nguyên lý của hình học và trình bày chúng dưới dạng các định lý và chứng minh logic.
Hình học phi Euclid:
Carl Friedrich Gauss, Nikolai Lobachevsky, và János Bolyai: Các nhà toán học này độc lập phát triển các lý thuyết về hình học phi Euclid, trong đó từ bỏ một số tiên đề của Euclid, đặc biệt là tiên đề về đường thẳng song song. Hình học phi Euclid mở ra những hướng đi mới trong toán học và vật lý.
Hình học giải tích:
René Descartes và Pierre de Fermat: Descartes và Fermat đã phát triển hình học giải tích, kết hợp hình học và đại số. Descartes giới thiệu hệ tọa độ Cartesian, cho phép biểu diễn các đường và hình dạng bằng các phương trình đại số.
Hình học vi phân:

Người phát minh ra tam giác vuông và công thức tính - Pythagoras
Carl Friedrich Gauss: Gauss đã có những đóng góp quan trọng trong hình học vi phân, nghiên cứu các tính chất của các bề mặt cong. Công trình của ông đã đặt nền móng cho lý thuyết về độ cong và hình học của không gian Riemann.
Bernhard Riemann: Riemann mở rộng hình học vi phân qua việc giới thiệu khái niệm về đa tạp và không gian Riemann. Các công trình của ông có ảnh hưởng lớn đến thuyết tương đối rộng của Albert Einstein.
Hình học topo:
Henri Poincaré: Poincaré là một trong những nhà sáng lập hình học topo, nghiên cứu các tính chất của các không gian mà không thay đổi qua các phép biến hình liên tục. Công trình của ông đã mở ra một lĩnh vực nghiên cứu mới trong toán học.
Lý thuyết hình học của thuyết tương đối:
Albert Einstein: Einstein đã sử dụng hình học phi Euclid trong thuyết tương đối rộng của mình, trong đó không gian và thời gian được mô tả bằng một đa tạp bốn chiều cong. Điều này đã cách mạng hóa sự hiểu biết của chúng ta về lực hấp dẫn và cấu trúc của vũ trụ.
Những phát minh và công trình này không chỉ đặt nền móng cho ngành hình học mà còn có ảnh hưởng sâu rộng đến nhiều lĩnh vực khác như vật lý, thiên văn học, và khoa học máy tính.