Hệ thức lượng trong tam giác vuông
Hệ thức lượng tam giác vuông là một tập hợp các công thức liên quan đến các cạnh và góc của tam giác vuông. Các hệ thức này giúp chúng ta giải quyết các bài toán về đo đạc và tính toán trong hình học.
Dưới đây là các công thức tính hệ thức lượng tam giác vuông, bao gồm định lý Pythagore và các tỉ số lượng giác. Những công thức này rất hữu ích trong việc giải quyết các bài toán liên quan đến tam giác vuông.
Định lý Pythagore
Trong một tam giác vuông, định lý này cho biết mối quan hệ giữa các cạnh:
Trong đó:
- c: Độ dài cạnh huyền (cạnh đối diện góc vuông).
- a và b: Độ dài hai cạnh góc vuông.
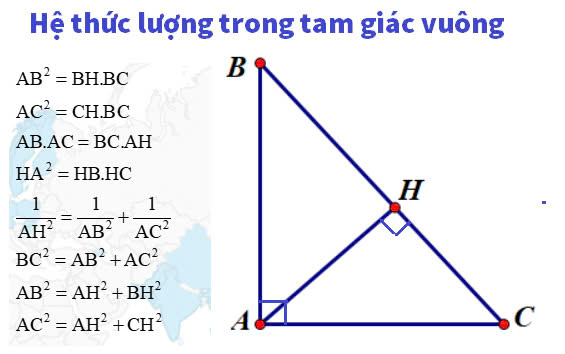
Công thức lượng tam giác vuôngCác tỉ số lượng giác
Tỉ số lượng giác cho một góc trong tam giác vuông:
Sin (sine):
sin A = cạnh đối diện góc A / cạnh huyền = a / c
Cos (cosine):
cos A = cạnh kề với góc A / cạnh huyền = b / c
Tan (tangent):
tan A = cạnh kề với góc A / cạnh đối diện góc A = b / a
Tỉ số lượng giác cho góc B (góc kề với A):
Sin:
sin B = cạnh đối diện góc B / cạnh huyền = b / c
Cos:
cos B = cạnh kề với góc B / cạnh huyền = a / c
Tan:
tan B = cạnh kề với góc B / cạnh đối diện góc B = a / b
Công thức tính góc
Khi biết cạnh, bạn có thể sử dụng các hàm lượng giác ngược để tính góc:
Tìm góc A:
A = sin⁻¹ (a/c) = cos⁻¹ (b/c) = tan⁻¹ (b/a)
Tìm góc B:
B = sin⁻¹ (b/c) = cos⁻¹ (a/c) = tan⁻¹ (a/b)
Hệ thức lượng cho tam giác vuông đặc biệt
Tam giác vuông 30-60-90:
- Cạnh đối diện góc 30° là một nửa cạnh huyền: a=c/2
- Cạnh đối diện góc 60° bằng √3 lần cạnh đối diện góc 30°: b = (√3/2).c
Tam giác vuông 45-45-90:
- Hai cạnh góc vuông bằng nhau: a=b
- Cạnh huyền bằng √2 lần độ dài cạnh góc vuông: c=a√2
Công thức Heron
Nếu bạn biết độ dài của cả ba cạnh trong một tam giác vuông (hoặc bất kỳ tam giác nào), bạn có thể sử dụng công thức Heron để tính diện tích:
- s= (a+b+c)/2 (nửa chu vi)
- Diện tích = √(s(s - a)(s - b)(s - c))
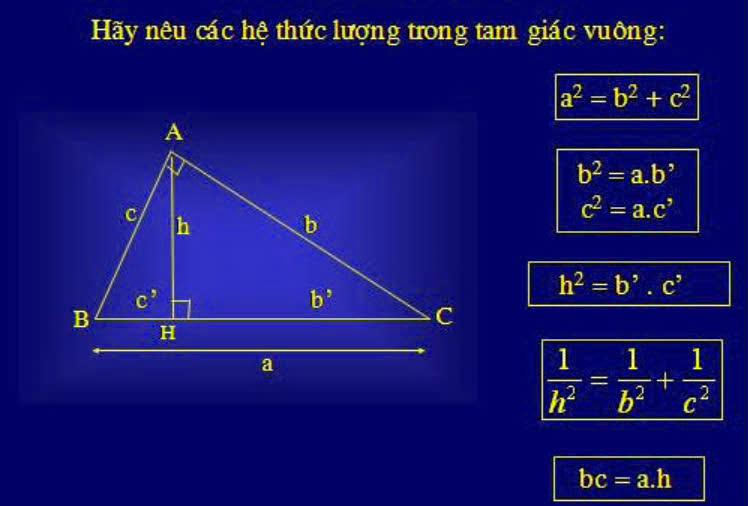
Các công thức tính hệ thức lượng tam giác vuôngĐể xác định xem một tam giác có phải là tam giác vuông hay không, bạn có thể sử dụng một trong những phương pháp sau đây:
Sử dụng Định lý Pythagore
Nếu bạn biết độ dài của ba cạnh a, b, và c (với c là cạnh dài nhất), bạn có thể kiểm tra định lý Pythagore:
c² = a² + b²
Nếu điều này đúng, thì tam giác là tam giác vuông.
Nếu không, tam giác không phải là tam giác vuông.
Kiểm tra các góc
Một tam giác vuông có một góc bằng 90 độ. Bạn có thể kiểm tra bằng cách đo góc hoặc sử dụng các phương pháp đo lường (như thước đo góc).
Sử dụng Tỉ số lượng giác
Nếu bạn biết các tỉ số lượng giác của các góc trong tam giác:
Nếu tanA hoặc tanB (với A và B là các góc) cho ra kết quả phù hợp với các cạnh của tam giác, bạn có thể xác định rằng góc đó là 90 độ.
Sử dụng định lý lượng giác
Nếu một trong các góc có sin bằng 1 (tức là sinA=1), thì góc đó là 90 độ, và do đó tam giác là tam giác vuông.
Phương pháp Kiểm tra Tính vuông
Nếu bạn có thể dựng một hình vuông trên một cạnh của tam giác và nhận thấy rằng cạnh còn lại chạm vào các đỉnh của hình vuông, thì tam giác đó là tam giác vuông.
Tham khảo: Đề thi tiếng anh thpt quốc gia 2019 mã 401
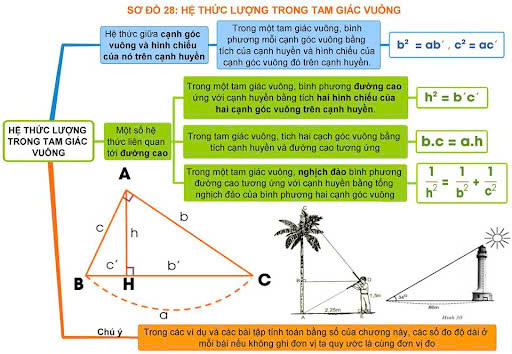
ví dụ về hệ thức lượng tam giác vuôngCác hệ thức lượng tam giác vuông, bao gồm định lý Pythagore và các tỉ số lượng giác (sin, cos, tan), có rất nhiều ứng dụng thực tế. Dưới đây là một số ví dụ phổ biến về cách những công thức này được sử dụng trong đời sống hàng ngày và trong các lĩnh vực khoa học, kỹ thuật:
Xây dựng và Kiến trúc
- Tính toán chiều dài và chiều cao: Trong xây dựng nhà cửa hoặc thiết kế các công trình, các nhà kiến trúc sư và kỹ sư thường sử dụng định lý Pythagore để xác định chiều cao, độ dốc của mái, hoặc chiều dài của các vật liệu cần thiết.
- Thiết kế cầu thang: Để đảm bảo cầu thang có độ dốc an toàn, các tỉ số lượng giác như tan góc của độ dốc được sử dụng để tính toán kích thước của bậc thang.
- Xác định độ vuông góc của các góc: Sử dụng định lý Pythagore để kiểm tra góc vuông trong quá trình đo đạc và thiết kế, đảm bảo các góc 90 độ, giúp công trình bền vững và thẩm mỹ.
Điều hướng và Hàng hải
- Tìm khoảng cách ngắn nhất: Trong hàng hải hoặc hàng không, người ta sử dụng định lý Pythagore để tính toán khoảng cách ngắn nhất giữa hai điểm trên mặt đất hoặc trên biển khi biết độ cao và khoảng cách ngang.
- Định vị và điều hướng: Sử dụng các tỉ số lượng giác để xác định góc và hướng di chuyển, giúp điều chỉnh đúng hướng đi và đảm bảo đến đích chính xác.
Trắc địa và Đo đạc
- Đo chiều cao của vật thể: Bằng cách đo góc nâng và khoảng cách từ vị trí đo đến chân vật thể, các nhà trắc địa có thể sử dụng tỉ số lượng giác (tan góc) để xác định chiều cao của một tòa nhà, ngọn núi hoặc cây cối.
- Xác định vị trí tương đối: Các hệ thức lượng tam giác vuông giúp tính toán khoảng cách và vị trí tương đối giữa các điểm trong công tác khảo sát địa hình.
Thiết kế Đồ họa và Công nghệ
- Tính toán vị trí và khoảng cách: Trong thiết kế đồ họa 2D, 3D, các nhà thiết kế sử dụng các tỉ số lượng giác để xác định vị trí, tỷ lệ và góc quay của các đối tượng.
- Định hướng góc nhìn camera: Các hệ thức lượng được sử dụng trong công nghệ mô phỏng và trò chơi để định hướng góc nhìn của camera và điều chỉnh các yếu tố hình ảnh theo chiều sâu.
Ứng dụng trong Toán học và Vật lý
- Tính lực và vận tốc: Trong vật lý, các thành phần vận tốc và lực thường được tính bằng cách sử dụng các tỉ số lượng giác. Ví dụ, khi một vật thể di chuyển theo hướng chéo, bạn có thể sử dụng sin và cos để tính toán lực theo trục x và y.
- Chuyển động dốc: Định lý Pythagore và các hệ thức lượng giác giúp tính toán các thành phần vận tốc khi một vật di chuyển trên mặt phẳng nghiêng.
Ứng dụng trong Đời sống Hằng ngày
- Sử dụng thang: Khi sử dụng thang để đạt đến một độ cao nhất định, người ta cần đặt thang ở góc an toàn để tránh bị trượt. Sử dụng tỉ số lượng giác (tan) để xác định góc đặt thang hợp lý.
- Đo khoảng cách khi không thể tiếp cận trực tiếp: Ví dụ, đo khoảng cách từ bờ đến một con thuyền trên biển bằng cách tính góc và sử dụng tan để suy ra khoảng cách thực.
Điện tử và Kỹ thuật Điện
- Tính toán dòng điện và điện áp: Các thành phần của dòng điện xoay chiều trong mạch điện thường được biểu diễn dưới dạng các tam giác vuông, và các tỉ số lượng giác giúp xác định mối quan hệ giữa dòng điện, điện áp và pha.
- Những ứng dụng này cho thấy hệ thức lượng tam giác vuông là một công cụ toán học quan trọng, không chỉ dùng trong các ngành khoa học kỹ thuật mà còn có giá trị trong đời sống hằng ngày.
Bài viết trên đã giới thiệu những kiến thức cơ bản về hệ thức lượng tam giác vuông, bao gồm các công thức và ứng dụng quan trọng như định lý Pythagore và các tỉ số lượng giác. Thông qua các ví dụ thực tế từ xây dựng, trắc địa đến kỹ thuật và đời sống, hy vọng rằng bạn đọc sẽ hiểu rõ hơn về giá trị và cách áp dụng của các hệ thức này. Mong rằng những kiến thức này sẽ trở thành công cụ hữu ích, giúp bạn giải quyết các bài toán hình học và các tình huống thực tiễn một cách tự tin và hiệu quả.
Nếu bạn cần thêm thông tin về dịch vụ marketing, hãy liên hệ với Kinh Bắc Media. Chúng tôi sẵn sàng hỗ trợ bạn với các giải pháp tiếp thị chuyên nghiệp và hiệu quả, giúp bạn đạt được mục tiêu kinh doanh và nâng cao nhận diện thương hiệu.
Thông tin chi tiết vui lòng liên hệ:
- Kinh Bắc Media
- Địa chỉ: Tầng 4 tòa nhà Thanh Long số nhà 134 Mai Anh Tuấn - Hồ Hoàng Cầu - Đống Đa - Hà Nội
- Hotline: 0969 024 600 / 024 62 733 721
- Website: https://www.kinhbacmedia.com/