Diện tích hình thang cân
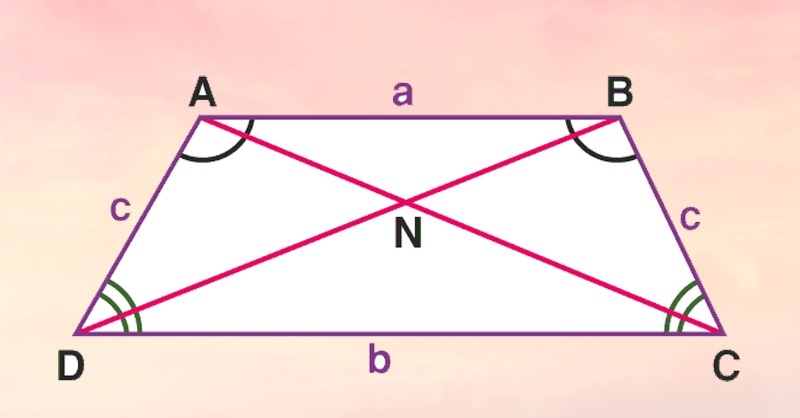
Hình thang cân là một loại hình thang đặc biệt trong hình học phẳng. Đặc điểm nhận dạng rõ nhất của hình thang cân là hai cạnh bên bằng nhau và hai góc kề cạnh đáy bằng nhau. Nhờ tính chất này, hình thang cân có sự đối xứng trục qua đường thẳng đi qua trung điểm của hai đáy.
Ngoài ra, trong hình thang cân:
Hai đường chéo luôn bằng nhau.
Trục đối xứng giúp chia hình thang cân thành hai phần bằng nhau.
Các góc ở đáy lớn và đáy nhỏ tương ứng bằng nhau.
Chính nhờ những đặc điểm nổi bật đó, hình thang cân thường được nhắc đến trong chương trình toán học THCS và có nhiều ứng dụng trong thực tế, đặc biệt trong kiến trúc và kỹ thuật.

Hình thang cân là một loại hình thang đặc biệtDiện tích của hình thang cân được tính theo công thức:
S=(a + b) x h / 2
Trong đó:
a: độ dài đáy lớn
b: độ dài đáy nhỏ
h: chiều cao (đo vuông góc giữa hai đáy)
Ví dụ:
Hình thang cân có a=10cm, b=6cm, h=5cm.
S=(10 + 6) x 5 / 2=40 cm²
Cách chứng minh công thức tính diện tích của hình thang cânĐể chứng minh công thức diện tích của hình thang cân, ta có thể dựa vào cách phân tích hình học cơ bản như sau:
Giả sử hình thang cân ABCD có AB // CD, với AB là đáy nhỏ, CD là đáy lớn, AD=BC là hai cạnh bên bằng nhau.
Kẻ chiều cao AH từ đỉnh A vuông góc với đáy lớn CD tại H, và kẻ BK từ đỉnh B vuông góc với CD tại K. Khi đó, AH=BK=h chính là chiều cao của hình thang cân.
Sau khi kẻ, hình thang cân ABCD được chia thành ba phần:
Hình chữ nhật ABKH.
Hai tam giác vuông cân là ΔADH và ΔBCK.
Gọi AB=b, CD=a, AH=h. Khi đó ta có:
Diện tích hình chữ nhật ABKH: S1=b x h.
Diện tích mỗi tam giác vuông: S2=1/2 x ((a – b)/2) x h.
Vì có hai tam giác bằng nhau, tổng diện tích của chúng là S3=(a – b)/2 x h.
Tổng diện tích của hình thang cân:
S=S1+S3
S=b x h+(a – b) x h / 2
S=(a + b) x h / 2
Công thức tính diện tích của hình thang cân được chứng minh rõ ràng như sau:
S=(a + b) x h / 2
Trong đó:
a là độ dài đáy lớn,
b là độ dài đáy nhỏ,
h là chiều cao kẻ vuông góc giữa hai đáy.

Ví dụ minh họa về diện tích của hình thang cânVí dụ 1:
Cho hình thang cân có đáy lớn a=12 cm, đáy nhỏ b=8 cm, chiều cao h=5 cm. Tính diện tích của hình thang cân đó.
Lời giải:
Áp dụng công thức:
S=(a + b) x h / 2
S=(12 + 8) x 5 / 2
S=20 x 5 / 2=50 cm²
Vậy diện tích của hình thang cân là 50 cm² .
Ví dụ 2:
Một hình thang cân có đáy lớn a=20 m, đáy nhỏ b=10 m và chiều cao h=7 m. Hãy tính diện tích mảnh đất có dạng hình thang cân này.
Lời giải:
S=(a + b) x h / 2
S=(20 + 10) x 7 / 2
S=30 x 7 / 2=105 m²
Vậy diện tích mảnh đất hình thang cân là 105 m² .
Ví dụ 3 (nâng cao):
Một hình thang cân có chu vi bằng 50 cm, đáy lớn a=18 cm, đáy nhỏ b=10 cm, hai cạnh bên bằng nhau. Hãy tính diện tích của hình thang cân biết chiều cao h=6 cm.
Lời giải:
Áp dụng công thức:
S=(a + b) x h / 2
S=(18 + 10) x 6 / 2
S=28 x 6 / 2=84 cm²
Vậy diện tích của hình thang cân là 84 cm² .
Ví dụ 4:
Một hình thang cân có đáy lớn CD=10 cm, đáy nhỏ AB=6 cm, chiều cao AH=5 cm.
Công thức tính diện tích: S=(a + b) x h / 2
S=(10 + 6) x 5 / 2=16 x 5 / 2=40 cm²
Ví dụ 5:
Hình thang cân có đáy lớn CD=12 cm, đáy nhỏ AB=8 cm, chiều cao AH=4 cm.
S=(12 + 8) x 4 / 2=20 x 4 / 2=40 cm²
Ví dụ 6:
Một hình thang cân có đáy lớn 15 cm, đáy nhỏ 9 cm, chiều cao 6 cm.
S=(15 + 9) x 6 / 2=24 x 6 / 2=72 cm²
Ví dụ 7 (bài tập nâng cao):
Hình thang cân có đáy nhỏ AB=7 cm, cạnh bên AD=BC=5 cm, đáy lớn CD chưa biết, chiều cao h=4 cm.
Nếu biết đáy lớn CD=11 cm, diện tích:
S=(11 + 7) x 4 / 2=18 x 4 / 2=36 cm²
Ví dụ 8 (bài tập ứng dụng):
Hình thang cân trong thực tế: mảnh đất hình thang cân có đáy lớn 20 m, đáy nhỏ 12 m, chiều cao 8 m. Diện tích đất:
S=(20 + 12) x 8 / 2=32 x 8 / 2=128 m²
Công thức tính diện tích của hình thang cân không chỉ là kiến thức lý thuyết trong sách giáo khoa, mà còn có rất nhiều ứng dụng thực tế trong đời sống, kỹ thuật và xây dựng:
Trong kiến trúc và xây dựng
Thiết kế mái nhà, cầu, đường dốc hay các công trình có hình dạng thang cân.
Tính diện tích bề mặt sàn hoặc diện tích lát nền có hình thang cân để chuẩn bị vật liệu chính xác.
Trong đo đạc và bản vẽ kỹ thuật
Xác định diện tích đất hoặc mảnh vườn hình thang cân để đo đạc đất đai.
Vẽ bản đồ, sơ đồ kỹ thuật với các hình thang cân để đảm bảo tỷ lệ chính xác.
Trong học tập và bài tập toán học
Giúp học sinh rèn luyện kỹ năng áp dụng công thức, tính toán nhanh và chính xác.
Dùng làm ví dụ minh họa trong các bài toán hình học phẳng.
Trong đời sống hàng ngày
Tính diện tích bể bơi, hồ chứa nước hoặc sân thể thao có hình thang cân.
Thiết kế các vật dụng có hình dạng thang cân như bàn, kệ, giàn giáo, sân khấu…
Hiểu và vận dụng đúng công thức diện tích của hình thang cân giúp tiết kiệm thời gian, đảm bảo độ chính xác và ứng dụng hiệu quả trong nhiều lĩnh vực từ học tập đến đời sống, xây dựng và kỹ thuật.
Qua bài viết, bạn đã hiểu rõ diện tích của hình thang cân, bao gồm công thức tính, cách chứng minh và các ví dụ minh họa cụ thể. Việc nắm chắc kiến thức này không chỉ giúp học sinh học tốt môn Toán mà còn ứng dụng hiệu quả trong đời sống, từ đo đạc, thiết kế đến xây dựng và các lĩnh vực kỹ thuật khác.