Diện tích hình thang cân
Diện tích của hình thang cân được tính theo công thức nào?
Diện tích của hình thang cân được tính theo công thức chung của hình thang:
S=(a + b) × h / 2
Trong đó:
a: độ dài đáy lớn
b: độ dài đáy nhỏ
h: chiều cao (khoảng cách vuông góc giữa hai đáy)
Ví dụ minh họa:
Một hình thang cân có đáy lớn a=10 cm, đáy nhỏ b=6 cm, chiều cao h=5 cm.
S=(10 + 6) × 5 / 2=16 × 5 / 2=40 cm²
Công thức này rất dễ áp dụng cho mọi bài tập tính diện tích của hình thang cân, giúp học sinh nắm vững kiến thức cơ bản trong hình học lớp 8.

Làm sao để chứng minh công thức tính diện tích của hình thang cânLàm sao để chứng minh công thức tính diện tích của hình thang cân?
Để chứng minh công thức diện tích của hình thang cân, ta thực hiện các bước sau:
Xác định hình thang cân
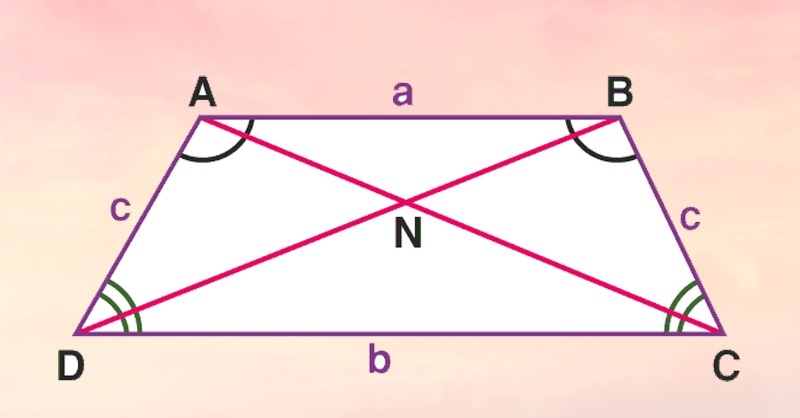
Giả sử hình thang cân ABCD có AB // CD, với AB là đáy nhỏ, CD là đáy lớn, AD=BC là hai cạnh bên bằng nhau.
Kẻ chiều cao
Kẻ chiều cao AH từ đỉnh A vuông góc với đáy lớn CD.
Tương tự, kẻ BK từ đỉnh B vuông góc với CD. Khi đó AH=BK=h là chiều cao của hình thang cân.
Chia hình thang thành các phần
Hình thang cân được chia thành:
Hình chữ nhật ABKH (với K là chân đường cao từ B).
Hai tam giác vuông cân ΔADH và ΔBCK.
Tính diện tích từng phần
Diện tích hình chữ nhật: S1=b × h
Diện tích mỗi tam giác vuông: S2=1/2 × ((a – b)/2) × h
Hai tam giác bằng nhau, tổng diện tích hai tam giác: S3=(a – b)/2 × h
Tổng diện tích của hình thang cân
S=S1+S3
S=b × h+(a – b) × h / 2
S=(a + b) × h / 2
Công thức diện tích của hình thang cân được chứng minh rõ ràng là:
S=(a + b) × h / 2
Trong đó:
a là đáy lớn
b là đáy nhỏ
h là chiều cao

Mẹo nhớ công thức hình thang Trong quá trình học và làm bài tập, có nhiều cách giúp tính diện tích của hình thang cân nhanh chóng, chính xác:
Sử dụng công thức chuẩn
Công thức cơ bản vẫn là:
S=(a + b) × h / 2
a: đáy lớn
b: đáy nhỏ
h: chiều cao
Đây là cách nhanh và phổ biến nhất khi biết đầy đủ đáy và chiều cao.
Tính bằng trung bình cộng của hai đáy nhân với chiều cao
Diện tích của hình thang cân cũng có thể hiểu là:
S=trung bình cộng hai đáy × chiều cao
Cách này giúp học sinh dễ hình dung: “ Diện tích của hình thang cân bằng diện tích hình chữ nhật có chiều cao h và đáy bằng trung bình hai đáy của hình thang” .
Sử dụng đường chéo hoặc cạnh bên
Trong một số bài toán, nếu biết cạnh bên và góc, có thể tính chiều cao h trước:
h=√ (AD² – ((a – b)/2)² )
Sau đó áp dụng công thức chuẩn S=(a + b) × h / 2 để nhanh chóng có diện tích.
Áp dụng trực tiếp các bài tập quen thuộc
Khi gặp bài toán lặp lại (ví dụ dạng đề kiểm tra, bài tập lớp 8), học sinh có thể ghi nhớ các mẹo:
Nếu đáy lớn gấp đôi đáy nhỏ, diện tích=3 × b × h / 2
Nếu đáy nhỏ bằng nửa đáy lớn, áp dụng công thức nhanh S=(a + a/2) × h / 2=3a × h / 4
Để tính diện tích của hình thang cân nhanh, quan trọng là nhớ công thức cơ bản và biết cách linh hoạt áp dụng các phương pháp tính chiều cao hoặc trung bình cộng hai đáy tùy theo thông tin bài toán.
Bài tập tính diện tích của hình thang cân lớp 8 thường gặpDưới đây là các dạng bài tập phổ biến giúp học sinh lớp 8 luyện tập và nắm vững công thức:
Dạng 1: Cho đáy và chiều cao, tính diện tích
Ví dụ: Hình thang cân có đáy lớn CD=12 cm, đáy nhỏ AB=8 cm, chiều cao h=5 cm.
Áp dụng công thức: S=(a + b) × h / 2
S=(12 + 8) × 5 / 2=20 × 5 / 2=50 cm²
Dạng 2: Cho cạnh bên và hai đáy, tính chiều cao rồi tính diện tích
Ví dụ: Hình thang cân có đáy lớn CD=10 cm, đáy nhỏ AB=6 cm, cạnh bên AD=BC=5 cm.
Tính chiều cao: h=√ (AD² – ((CD – AB)/2)² )=√ (5² – (4/2)² )=√ (25 – 4)=√ 21 ≈ 4, 58 cm
Tính diện tích: S=(10 + 6) × 4, 58 / 2 ≈ 36, 64 cm²
Dạng 3: Tính diện tích khi biết đường chéo hoặc góc
Ví dụ: Hình thang cân có đáy nhỏ AB=6 cm, đáy lớn CD=10 cm, góc ở đáy nhỏ α=60°
Tính chiều cao h=AB × tan(α)=6 × tan60° ≈ 10, 39 cm
Diện tích: S=(6 + 10) × 10, 39 / 2 ≈ 83, 12 cm²
Dạng 4: Bài toán ứng dụng thực tế
Ví dụ: Một mảnh đất hình thang cân có đáy lớn 20 m, đáy nhỏ 12 m, chiều cao 8 m.
Tính diện tích đất: S=(20 + 12) × 8 / 2=128 m²
Những bài tập này giúp học sinh thực hành linh hoạt công thức S=(a + b) × h / 2, áp dụng trong nhiều trường hợp khác nhau từ lý thuyết đến thực tế. Việc luyện tập thường xuyên sẽ giúp tính toán nhanh và chính xác hơn.
Công thức diện tích của hình thang cân không chỉ là kiến thức lý thuyết trong sách giáo khoa mà còn được áp dụng rộng rãi trong đời sống, xây dựng và kỹ thuật.
Trong kiến trúc và xây dựng
Tính diện tích mái nhà, cửa sổ hình thang cân.
Tính diện tích mặt nghiêng của các công trình kiến trúc có hình dạng thang cân.
Giúp xác định vật liệu cần dùng chính xác, tránh lãng phí.
Trong đo đạc đất đai và nông nghiệp
Xác định diện tích mảnh đất hình thang cân để lập bản đồ, phân chia ruộng vườn.
Tính diện tích ao hồ, sân bãi có hình dạng tương tự.
Trong kỹ thuật và thiết kế
Tính diện tích các chi tiết máy hoặc bộ phận kỹ thuật có hình thang cân.
Sử dụng trong thiết kế đường dốc, băng tải hay mái che công nghiệp.
Trong học tập và giải toán thực tế
Giúp học sinh nắm vững kiến thức hình học và áp dụng công thức tính diện tích vào các bài toán thực tế.
Tăng khả năng tư duy, trực quan hình học, dễ dàng giải các bài tập kiểm tra.
Kết luận:
Công thức S=(a + b) × h / 2 không chỉ giúp tính diện tích của hình thang cân một cách nhanh chóng mà còn có ứng dụng rộng rãi trong đời sống thực tế, từ kiến trúc, xây dựng đến kỹ thuật và giáo dục. Việc nắm chắc công thức này mang lại sự chính xác và hiệu quả trong nhiều lĩnh vực.