Trọng tâm là gì
Trong vật lý, trọng tâm là một điểm tưởng tượng trong vật thể mà toàn bộ khối lượng của vật được coi như tập trung tại đó. Nói cách khác, nếu đặt vật thể lên một điểm tựa tại trọng tâm, vật sẽ cân bằng hoàn hảo mà không bị nghiêng. Trọng tâm giúp giải thích cách vật thể duy trì thăng bằng, chịu lực và chuyển động dưới tác dụng của trọng lực hoặc các lực khác.
Điểm đặc biệt là trọng tâm không nhất thiết phải nằm trong vật thể, đặc biệt với các vật thể hình dạng bất quy tắc hoặc rỗng. Ví dụ, một thanh cong hoặc móc treo hình chữ U có thể có trọng tâm nằm ngoài hình dạng thực của vật.
Hiểu rõ trọng tâm không chỉ quan trọng trong học tập mà còn ứng dụng rộng rãi trong xây dựng, thiết kế kết cấu, thể thao, vận tải và sinh hoạt hàng ngày. Nó giúp dự đoán chính xác cách vật thể sẽ nghiêng, lật hay duy trì thăng bằng khi chịu lực.
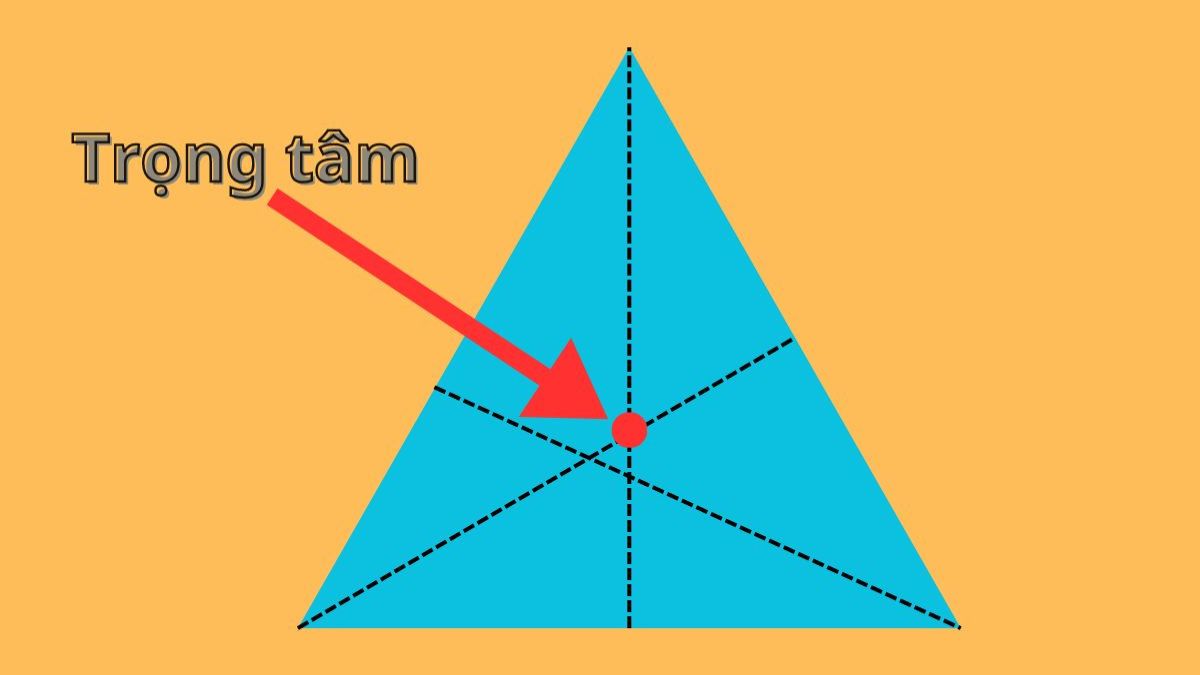
Định nghĩa trọng tâmTrọng tâm là gì? Trọng tâm là điểm mà toàn bộ khối lượng của vật thể được coi như tập trung. Cách tính trọng tâm phụ thuộc vào hình dạng và phân bố khối lượng của vật thể.
Trọng tâm của vật rắn đồng chất, hình học đơn giản
Hình chữ nhật, hình vuông: trọng tâm tại giao điểm hai đường chéo
Hình tam giác: trọng tâm tại giao điểm ba trung tuyến
Hình tròn hoặc hình trụ đều: trọng tâm tại tâm hình học
Trọng tâm của vật rắn không đồng chất hoặc hình dạng phức tạp
Khi khối lượng phân bố không đều, trọng tâm được xác định bằng công thức tổng quát:
x_ct=(Σ m_i * x_i) / Σ m_i
y_ct=(Σ m_i * y_i) / Σ m_i
z_ct=(Σ m_i * z_i) / Σ m_i
Trong đó:
m_i: khối lượng từng phần tử nhỏ
x_i, y_i, z_i: tọa độ từng phần tử
(x_ct, y_ct, z_ct): tọa độ trọng tâm
Công thức tích phân cho vật thể liên tục
x_ct=∫ x dm / ∫ dm
y_ct=∫ y dm / ∫ dm
z_ct=∫ z dm / ∫ dm
dm: phần tử khối lượng vô cùng nhỏ của vật thể
Công thức này áp dụng cho vật thể liên tục và hình dạng phức tạp
Lưu ý:
Tất cả các phần tử phải đo theo cùng một hệ trục tọa độ.
Với vật thể phức tạp, có thể chia vật thành nhiều phần nhỏ, tính trọng tâm từng phần, sau đó áp dụng công thức tổng quát.

Công thức trọng tâmrong vật lý và đời sống thực tế, trọng tâm có thể phân loại dựa trên hình dạng vật thể và phân bố khối lượng. Hiểu các loại trọng tâm giúp xác định cân bằng và ứng dụng vào thực tiễn hiệu quả.
Trọng tâm của vật rắn đồng chất
Áp dụng cho các vật thể có khối lượng phân bố đều.
Trọng tâm thường nằm tại tâm hình học hoặc giao điểm các đường đối xứng.
Ví dụ: hình vuông, hình chữ nhật, hình tròn, hình trụ đều.
Trọng tâm của vật rắn không đồng chất
Dành cho vật có khối lượng phân bố không đồng đều.
Trọng tâm nghiêng về phía phần nặng hơn.
Ví dụ: thanh có một đầu nặng hơn, hoặc vật hình dạng bất quy tắc.
Trọng tâm của vật lỏng
Trong chất lỏng, trọng tâm thường trùng với tâm khối lượng của chất lỏng, ảnh hưởng đến thăng bằng thuyền, tàu hoặc các thùng chứa.
Trọng tâm của vật thể hình dạng bất quy tắc
Các vật thể rỗng, cong, hay không đồng chất.
Trọng tâm có thể nằm ngoài vật thể, ví dụ móc treo chữ U hoặc thanh cong.
Thường phải xác định bằng phương pháp thực nghiệm hoặc tích phân.
Hiểu các loại trọng tâm giúp áp dụng trong thiết kế, xây dựng, thể thao, vận tải và các bài toán vật lý, đảm bảo cân bằng, ổn định và an toàn.
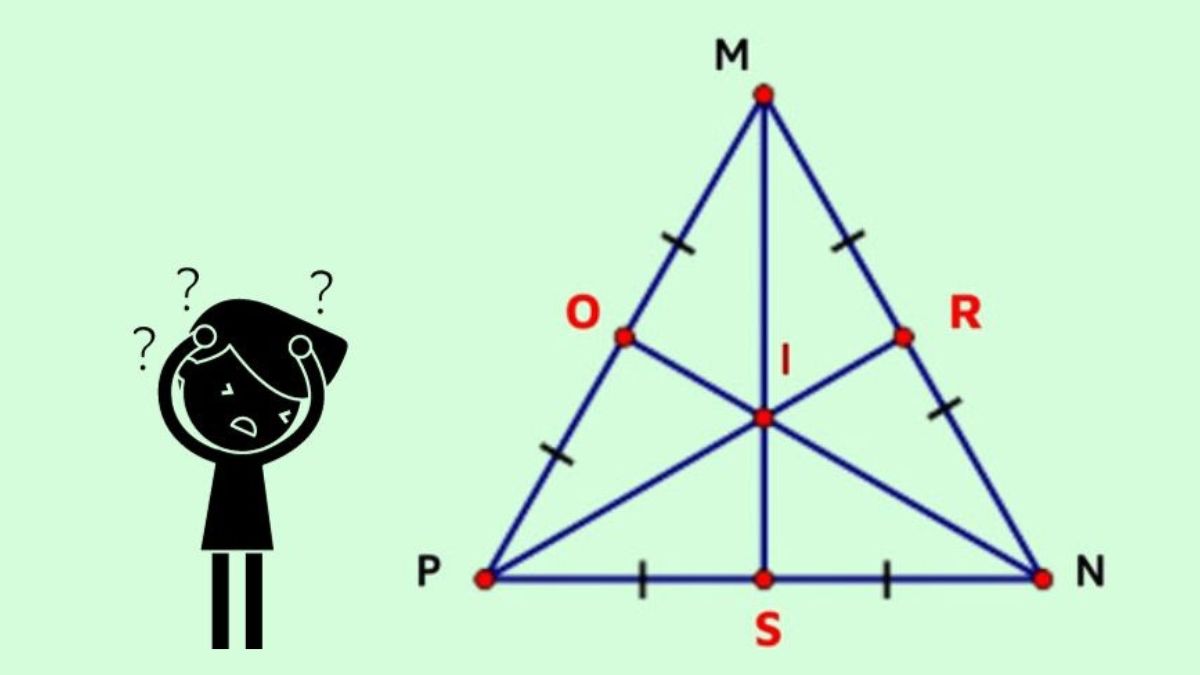
Các loại trọng tâm thường gặpXác định trọng tâm giúp hiểu cách vật thể cân bằng và chuyển động. Phương pháp xác định phụ thuộc vào hình dạng và phân bố khối lượng của vật thể.
Trọng tâm của vật rắn đồng chất, hình học đơn giản
Với các vật thể đồng chất và hình dạng cơ bản như hình chữ nhật, hình vuông, hình tam giác, hình tròn, trọng tâm thường nằm ở giao điểm các đường đối xứng hoặc trung tuyến.
Ví dụ:
Hình chữ nhật: trọng tâm tại giao điểm hai đường chéo
Hình tam giác: trọng tâm tại giao điểm ba trung tuyến
Trọng tâm của vật rắn không đồng chất hoặc hình dạng phức tạp
Khi khối lượng phân bố không đều, trọng tâm sẽ nghiêng về phía phần nặng hơn.
Có thể tính trọng tâm bằng công thức tổng quát:
x_ct=(Σ m_i * x_i) / Σ m_i
y_ct=(Σ m_i * y_i) / Σ m_i
z_ct=(Σ m_i * z_i) / Σ m_i
Trong đó:
m_i là khối lượng của từng phần tử nhỏ
x_i, y_i, z_i là tọa độ từng phần tử
(x_ct, y_ct, z_ct) là tọa độ trọng tâm
Phương pháp thực nghiệm xác định trọng tâm
Treo vật thể từ một điểm cố định và thả dây thẳng đứng, vẽ đường theo dây treo.
Treo từ một điểm khác và vẽ tiếp đường thẳng.
Giao điểm của hai đường này chính là trọng tâm.
Phương pháp này rất hữu ích với các vật thể bất quy tắc hoặc khi làm thí nghiệm vật lý, giúp xác định trọng tâm nhanh chóng và chính xác.
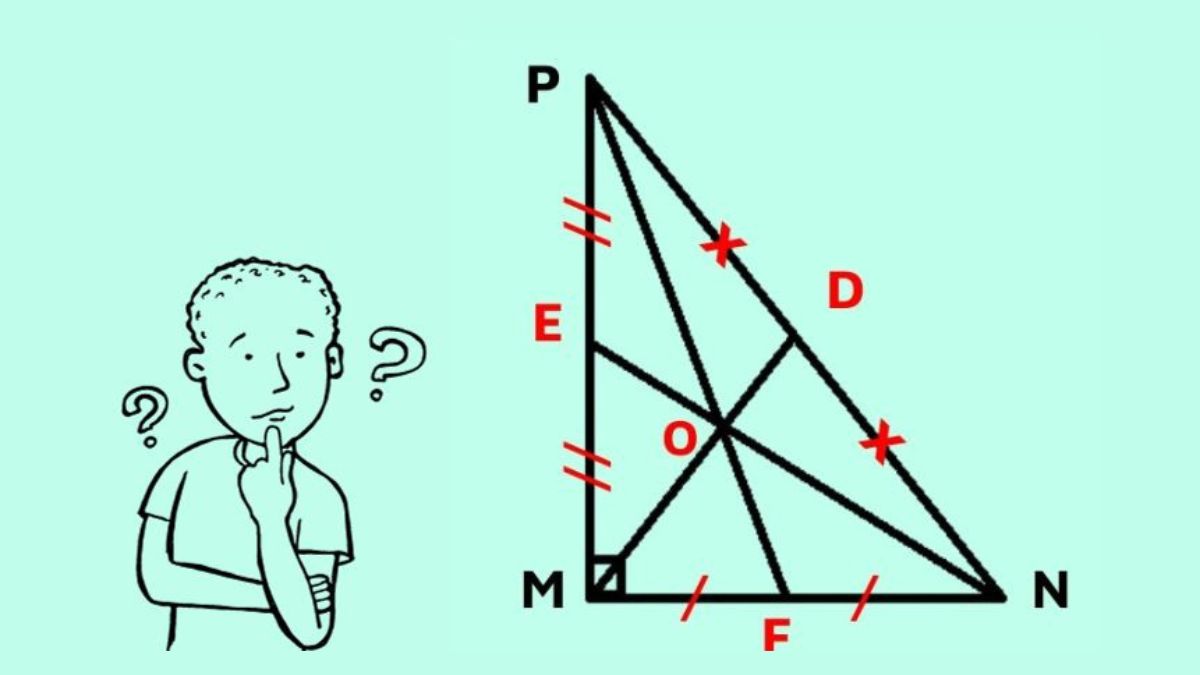
Ví dụ về trọng tâm trong đời sống và ứng dụng thực tếTrọng tâm là gì? Hiểu rõ trọng tâm không chỉ giúp giải các bài toán vật lý mà còn có ứng dụng rộng rãi trong đời sống và nhiều lĩnh vực kỹ thuật.
Trong xây dựng và thiết kế kiến trúc
Khi thiết kế tòa nhà, cầu hay các kết cấu lớn, kỹ sư cần xác định trọng tâm để đảm bảo cân bằng và ổn định.
Một tòa nhà với trọng tâm thấp và phân bố khối lượng hợp lý sẽ ít bị nghiêng hoặc lật khi chịu gió mạnh hoặc động đất.
Trong thể thao và vận động
Vận động viên như trượt băng, thể dục dụng cụ, nhảy cao sử dụng kiến thức trọng tâm để duy trì thăng bằng và kiểm soát chuyển động.
Ví dụ: khi nhảy cao, việc hạ thấp trọng tâm giúp cơ thể ổn định trên không trung.
Trong giao thông và vận tải
Xe tải hoặc container cần sắp xếp hàng hóa sao cho trọng tâm càng thấp càng tốt, giảm nguy cơ lật xe khi di chuyển.
Phân bố khối lượng hợp lý giúp xe chạy an toàn và tiết kiệm nhiên liệu.
Trong đời sống hàng ngày
Khi xếp đồ đạc, sách vở hay các vật nặng lên kệ, tủ, biết trọng tâm giúp sắp xếp hợp lý để tránh đổ ngã.
Ví dụ: đặt vật nặng ở phần dưới kệ sẽ tạo trọng tâm thấp, tăng tính ổn định.
Những ví dụ trên cho thấy việc hiểu rõ trọng tâm không chỉ là kiến thức lý thuyết mà còn rất thiết thực, giúp đảm bảo cân bằng, ổn định và an toàn trong nhiều hoạt động đời sống và kỹ thuật.
Hiểu rõ trọng tâm là gì giúp chúng ta nắm vững kiến thức về cân bằng, chuyển động và phân bố khối lượng của vật thể. Từ bài tập vật lý đến ứng dụng trong xây dựng, thể thao, giao thông hay đời sống hàng ngày, việc xác định trọng tâm đúng cách mang lại sự ổn định, an toàn và hiệu quả. Nắm vững kiến thức này không chỉ hỗ trợ học tập mà còn giúp lập kế hoạch, thiết kế và sắp xếp vật thể hợp lý trong thực tế.